Number of winding symmetries
The number of winding symmetries indicates the number of rotational symmetries in the winding layout. It indicates also the machine periodicity.
The number of winding symmetries is calculated as the greatest common divisor (GCD) between the number of slots and the number of pole pairs:
$$ GCD \left( Q_s, \frac{p}{2} \right) $$Examples:
A 6-pole 9-slot winding has 3 symmetries.
A 8-pole 12-slot winding has 4 symmetries.
A 8-pole 18-slot winding has 2 symmetries.
Regarding the number of winding symmetries or machine periodicity, the conductor orientation is taken into account. The inverse of the number of symmetries displayed in the Emetor winding calculator is the fraction of the machine that should be modeled in a finite-element program whenever there is some current in the winding coils (i.e. load simulations). When there is a negative magnetic periodicity, such as for integer-slot windings and for some double-layer concentrated windings with an even number of stator slots, the number of symmetries is double that calculated with the equation above. On the contrary, for some single-layer concentrated windings, the effective number of symmetries might only be half of that calculated. That said, the number of winding symmetries displayed in the winding calculator is only an indicative value. For a better estimate, you would have to look at the specific winding layout.
If the number of winding symmetries is equal to 1, then there are no symmetries in the winding. Be aware of unbalanced magnetic forces, vibration and noise in this case that might be an issue, refer to Fig. 1 below.
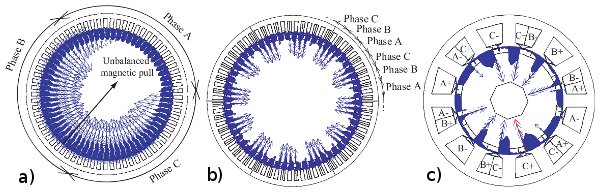
Fig. 1 Magnetic forces on the stator of a permanent-magnet synchronous motor: a) 68-poles 69-slots with a winding symmetry of 1, b) 60-poles 72-slots with 6 winding symmetries, c) 10-poles 12-slots with a winding symmetry of 1, but with a negative periodicity [1].
References:
[1] Florence Meier, Permanent-Magnet Synchronous Machines with Non-Overlapping Concentrated Windings for Low-Speed Direct-Drive Applications, Phd Thesis, Royal Institute of Technology (KTH), July 2008 ![]()
Read about another glossary term
