Stacking factor

The stacking factor is the ratio of electrical steel along the axial length of the iron core.

The magnetic core of electrical machines is often made up of thin iron laminations in order to reduce eddy-current losses and improve the performance. These lamination sheets are slightly insulated with a coating and are oriented in parallel with the direction of the magnetic flux. Laminating a core increases its volume not only due to the applied coating, but also since the stacked laminations are not perfectly flat due to manufacturing or processing, e.g. punching.

It is important to account for the stacking factor when designing an electrical machine, since a stacking factor of less than 1.0 reduces the flux carrying capacity of the iron core accordingly. The stacking factor is low for very thin iron laminations and is approaching unity as the lamination thickness increases. The stacking factor is sometimes also called lamination factor or space factor.

In order to get a reasonable estimate of the stacking factor, check the electrical steel database for your specific material or use the following rule of thumb that Emetor uses in order to estimate the stacking factor when there is no value available from the manufacturer.

Rule of thumb for calculating the stacking factor as a function of the lamination thickness

Not many producers of electrical steel do provide the stacking factor for their lamination sheets. This is fully understandable since the stacking factor depends a lot on the manufacturing process, i.e. the punching and stacking of the lamination sheets. Still, the rule of thumb for calculating the stacking factor as a function of the lamination thickness presented below might be a valuable first estimate for any electrical machine designer.

In many electrical machine design programs, the stacking factor is an input that many users have difficulties to estimate. However, it is important to account for the stacking factor when designing an electrical machine, since a stacking factor of less than 1.0 reduces the flux carrying capacity of the iron core accordingly. Hopefully, the following rule of thumb does help you to get a first estimate of the stacking factor: $$0.0425\cdot \delta _{lam} + 0.6032\cdot \mathrm{arctan} (108.16\cdot \delta _{lam})$$ where $\delta _{lam}$ is the lamination thickness given in mm.

The above equation is based on several sources of stacking factor estimates [1-4], as shown in Fig. 1. The same figure does also show the rule of thumb function, which was obtained by least-square curve-fitting of the available estimates.

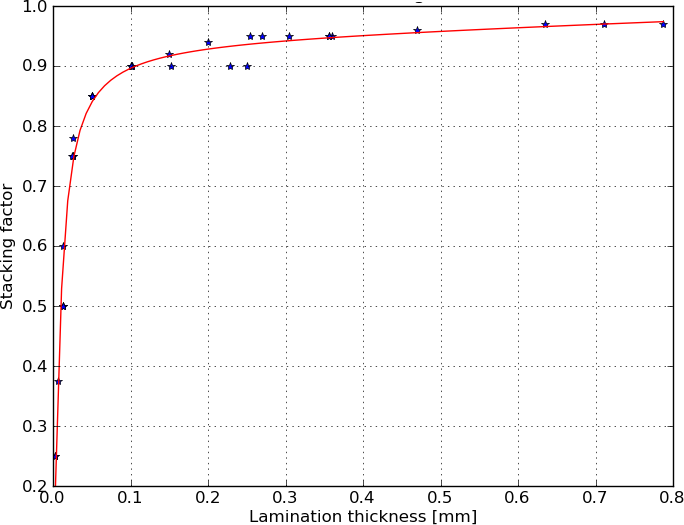
Estimates of stacking factors

Fig. 1 Estimates of stacking factor and rule of thumb function.

Examples

Based on the rule of thumb, the following stacking factors are estimated for some common lamination thicknesses:

Validity

The rule of thumb is based on stacking factor estimates in a range between 0.003mm and 0.8mm. For lamination sheets thicker or thinner than these values, the rule of thumb might not be applicable.

The rule of thumb ought to be reasonable for relatively small electrical machines professionally constructed with stacked laminations. For larger electrical machines with interleaved lamination sheets, which might become necessary if the machine dimensions exceed the available width of the lamination sheets, the stacking factor might be considerably lower than the one given by the rule of thumb.

References of lamination stacking factor estimates:
[1] R. E. Tarter, "Solid-State Power Conversion Handbook", Wiley-Interscience, 1993.
[2] S. A. Nasar, "Electric Machines & Electromechanics", McGraw-Hill, 1997.
[3] Magnetics Inc., "Core Selection for Saturating Transformers".
[4] Telcon Inc., "Toroidal cores".

Modeling a stack of laminations in the finite element method

This section explains how the iron core of an electrical machine consisting of stacked laminations can be modeled in the finite element method (FEM). The method is equally applicable for 2D- and 3D-FEM.

The proposed method for modeling a stack of laminations is based on section 7.4.1 of the book "Finite Element Analysis of Electrical Machines" by Sheppard J. Salon, Springer, 1995. According to the left hand side of Fig. 2, the core of many electrical machines consists of a series of iron lamination, with some unavoidable air gap and insulation coating in between. This reduces the flux carrying capacity of the iron core. The stacking factor $k_{st}$ is a measure of the ratio of electrical steel along the axial length of the iron core: $$k_{st} = \frac{l_{iron}}{l_{iron}+l_{air}}$$

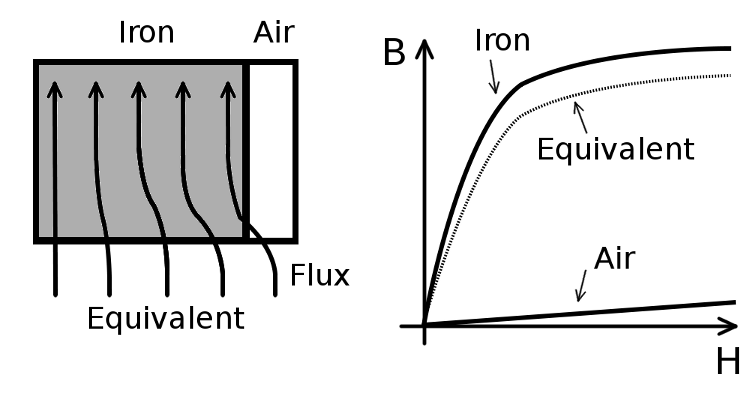
Modeling a stack of laminations

Fig. 2 Modeling a stack of laminations by an equivalent homogenous material

In order to model a stack of laminations in the finite element method, an equivalent homogenous material with the same macroscopic properties as the entire stack is created. If the magnetic flux is oriented in parallel with the direction of the lamination sheets, the equivalent permeability of the homogenous material becomes: $$\mu _{eq} = k_{st}\cdot \mu _{iron} + (1-k_{st})\cdot \mu _0$$ On the right hand side of Fig. 2 it is shown how the saturation curve can be altered in order to account for the stacking factor by applying the above equation to each point in the saturation curve.

However, in order to estimate the core losses in the iron laminations, it is essential to know the corresponding flux densities. Looking at the left hand side of Fig. 2, it is obvious that the flux density in the lamination sheet is higher than in the equivalent homogenous material. Therefore, the flux density in the iron $B_{iron}$ is derived from the equivalent flux density $B_{eq}$ as: $$B_{iron} = \frac{\mu _{iron}}{\mu _{eq}} B_{eq}$$ It is left to the reader to derive the above equation.

The stacking factor is generally used to calculate the following properties:

If the iron core of an electrical machine is made of stacked laminations, this can have a major influence on the machine performance, especially if the lamination thickness is very thin. In case you don't want to include the effect of the stacking factor in your simulations or you utilize a massive iron core, just put the stacking factors to the value 1.0.

Read about another glossary term